The development of engineering geophysics methods in the Bezvodnoe test area (privacy of the Institute of Applied Physics)
The site for geophysical experiments in the Bezvodnoe test area was equipped with the help of Vyacheslav Averbakh and Boris Bogolyubov in the late nineties to test the promising sources of coherent s
eismic radiation (designed by Bogolyubov) intended for solving a variety of problems in applied geophysics. Photos in Fig. 1.5 show the participants in the research missions, their work and the beauty of this place near a picturesque bank of the river Volga.
 |
Figure 2.5: Geophysical test area Bezvodnoe (privacy of the Institute of Applied Physics). On the photo from left to right is the staff: Alexander Stromkov, Andrey Lebedev, Andrey Konkov, Nikolay Vasilinenko, and Sergey Manakov. |
In the mid-nineties, Prof. Vladimir Talanov, Academician of the RAS, suggested that the multi-year hydroacoustic research expertise with coherent sources should be applied to analyzing the structure of the Earth’s surface layers. In 1996 Andrey Lebedev and Alexander Sutin proposed a scheme for coherent excitation of the seismic radiation by two resonant systems matched with the medium and with each other [1] (the possibility to use the volume source without matching resonant circuits was analyzed in [2]). The resulting estimates showed that the radiation power is limited by the cavitation strength of the liquid filling the matching element and can reach several kilowatts. However, this scheme had obvious drawbacks, namely, the need for accurate matching of resonators, a narrow emission band, and bulky design. Actually, such a scheme is suitable for the creation of stationary points of radiation which operate in the interferometer mode, for example, in the regions with a high level of seismicity for monitoring of the state of the geo medium.
The idea of excitation of seismic waves from natural reservoirs was implemented in an experiment on the river Trotsa (Nizhny Novgorod region) in 1998. The experiment showed the high efficiency of the wave excitation [3, 4]. Since the river bed of lowland rivers is covered with soft alluvial rocks, the bottom is relatively transparent and soft for acoustic waves. This provides a broad band of seismoacoustic emission [3]. More recently, we studied the coherent sounding of artificial and natural heterogeneities (problems in seismic tomography) [5-7], which showed good prospects for using coherent sources in the seismic exploration. We would especially like to acknowledge the work [5], in which Yury Postoenko solved the problem of imaging of an underground tunnel. The results obtained are shown in Fig. 2.6.
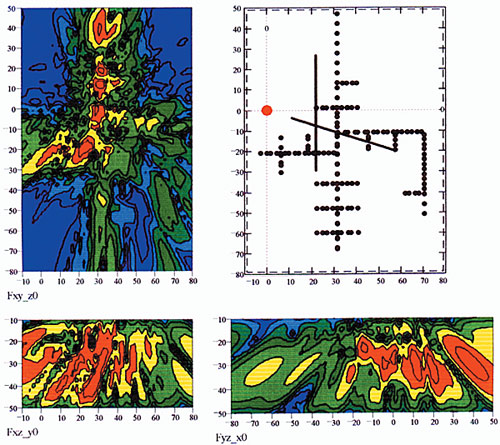
Figure 2.6. Seismoacoustic “imaging” of an underground tunnel. |
Shown on the top right is the location of the measurement system elements relative to the tunnel (the source location is marked with a red symbol, the geophone locations, with lines, and the tunnel outlines, with black dots). The sections (tomograms) of a tunnel obtained as a result of coherent processing (focusing) are shown in Fig. 2.6 as a distribution of “acoustic” brightness. Work [5] was in fact the starting point for the research line associated with the solution of the dynamic inverse problems and the development of methods for remote diagnostics and monitoring (see the text below).
The use of high-power coherent sources yielded interesting results on the nonlinear wave interaction in fractured granite forming the shore of the lake Ladoga [8]. The obtained estimate of the acoustic nonlinearity coefficient was later confirmed by the method of acoustic spectroscopy under laboratory conditions [9]. Examples of using coherent sources of seismoacoustic radiation are presented in Fig. 2.7.
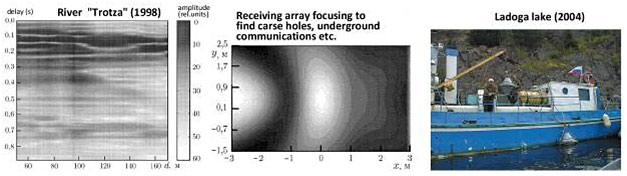
Figure 2.7. Examples of using the seismoacoustic emission coherence to solve the profiling problems (on the left is the experiment on the river Trotsa in 1998) and search for local heterogeneities (at the center is the experiment in the city of Sarov in 2001). Shown on the right is work during the Ladoga mission in 2004, namely, the lowering of a high-power hydroacoustic source designed by Bogolyubov.
In the late nineties Boris Bogolyubov developed a low-power electrodynamic vibrational source for engineering seismic survey [10] (afterwards we found out that at about the same time a source of a similar design was developed by our foreign colleagues for the solution of the same problems [11]). The possibility of localization of artificial local heterogeneities and solution of the problems of shallow profiling with this source was demonstrated in [10] (Fig. 2.7, center, taken from this work). A number of other interesting results obtained using the coherence of the seismoacoustic emission are presented in review [4].
In [12], a portable vibrational source was employed for local (in the acoustic impedance measurements) diagnostics of the ground state directly under the vibrator plate. The possibility to assess the degree of friability of the soil (Fig. 2.8) was demonstrated and the conditions for long-term stability (coherence) of the vibrational source were specified.
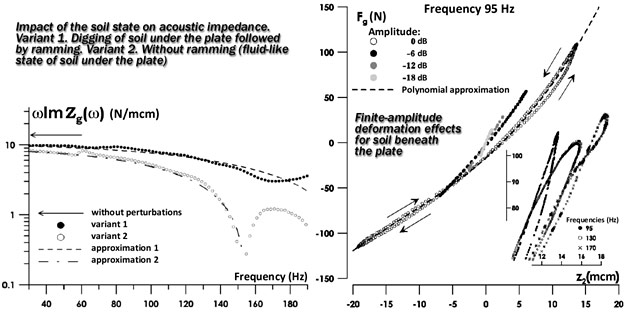
Figure 2.8. Examples of in-situ diagnostics of the soil state by measuring the input acoustic impedance of the medium.
It is interesting to note that the assessment of the Poisson ratio for the soil in the unperturbed state and the soil after loosening and subsequent ramming gives almost the same value (i.e., the structure of internal connections while ramming is recovered) and the Poisson ratio of the soil right after the loosening is close to 0.49 (semi-liquid state). Thus, the acoustic impedance measurements make it possible to assess the level of the effects on the ground. It was also demonstrated in the experiment [12] while comparing the data obtained in two years that the state of soil can be diagnosed depending on the evolution of the environment state (temperature and humidity). The surface roughness (typical grain size) was determined using the acoustic measurement data for a large-amplitude excitation. The very idea of ??determining the roughness by a nonlinear acoustic response is not new. The concept was analyzed in, e.g., [13] and then considered for the problems of applied geophysics to enhance the resolution of seismic survey using commercial vibrators [14, 15]. The experiment [12] is of interest due to the fact that the grain size evaluation obtained from in-situ acoustic data was found to be in very good agreement with direct observations of the soil particles under a microscope. The response itself is shown in Fig. 2.8 (the radiation losses, whose magnitude is independent of the oscillation amplitude, were subtracted). The hysteresis of the force-displacement (stress-strain) dependence is evident. It is interesting to note that, as far as we can judge based on the analysis of the literature, such in-situ dynamic characteristics of the soil were obtained for the first time. The following effects were observed: (1) the dynamic stiffness of the medium reduces with increasing amplitude; (2) the constant component determining the vibrator penetration (positive values ??z2 on the graph) increases during oscillations; (3) the hysteresis loops have a complex structure as the vibration frequency is varied, which apparently points to the features of the relaxation processes. In the sequel it is expected to continue research in this direction.
Special attention should be given to the development of non-conventional methods of seismic survey, and in particular to the use of SH waves in the cross-well profiling. This type of the wave motion is relatively rarely used in geophysics due to the technical difficulties of excitation. The design of a borehole source of SH waves is described in [16]. The source of a similar design was implemented in the experiment with phase profiling of the layered structure with a low contrast between parameters (Bezvodnoe test area, 2008) [17]. The use of phase methods of measurement, which are among the most accurate ones, in the conventional geophysics is limited by a long-term stability of the radiation sources. Under conditions of the Bezvodnoe test area (Fig. 2.9) it was possible to resolve a low contrast of the layers consisting of sandy clay, sandy loam, and clay. At the same time, the standard methods are not suitable due to a strong attenuation and therefore cannot provide the required emission band at long distances. Figure 2.9 on the left depicts geological data for the Bezvodnoe test area and on the right, the measured integral velocities of propagation and the result of the recovery of the shear wave velocity profile as a function of depth. The position of the boundaries is in satisfactory agreement with the geological data, and the velocity values, with the average values known from the literature ??for sandy loam, sandy clay, and clay (see. e.g., [18]).
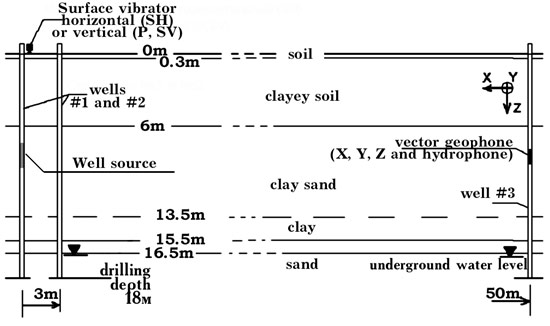
Figure 2.9. Phase profiling of low-contrast layers on the SH waves.
In 2009, the studies aimed at solving the dynamic inverse problems for in-situ determination of the parameters of the natural media and supported by the Russian Foundation for Basic Research were started. In the future we intend to create circuits for monitoring of the state of such media. An interesting generalization of the well-known method of spectral analysis of surface waves (abbr. SASW) was found during the studies. It appears that if, along with the dispersion dependence of the Rayleigh wave velocity, the frequency dependence of the projections ratio of the daylight surface displacement is included in the inversion algorithm, the recovery of the shear wave velocity profile and the Poisson ratio become possible. The comparison between two experiments conducted in 2009 and 2011 has demonstrated the ability to diagnose the saturation of a natural granular medium with liquid [19].
References to Section 2
1. Lebedev A, Sutin A (1996) Excitation of Seismic Waves by an Underwater Sound Projector. Acoustical Physics 42(6): 812–818.
2. Averbakh V, Zaslavsky Yu (1997) Spatio-Angular Characteristics and the Energy Balance of the Elastic Waves Excited in the Semi-Space by a Source of the Expansion-Center Type. Izvestiya, Physics of the Solid Earth 12: 1–5.
3. Averbakh V, Bogolyubov B, Dubovoi Yu, Zaslavsky Yu, Lebedev A, Maryshev A, Nazarov V, Pigalov K, Talanov V (2002) Application of Hydroacoustic Radiators for the Generation of Seismic Waves. Acoustical Physics 48(2): 149–155.
4. Lebedev A, Malekhanov A (2003) Coherent Seismoacoustics. Radiophysics and Quantum Electronics 46(7): 579–597.
5. Averbakh V, Artel’nyi V, Bogolyubov B, Zaslavsky Yu, Kukushkin V, Lebedev A, Maryshev A, Postoenko Yu, Talanov V (2001) Seismoacoustic Survey of Artificial Heterogeneities in the Ground. Acoustical Physics 47(4): 437–441.
6. Averbakh V, Bogolyubov B, Zaslavsky Yu, Lebedev A, Maryshev A, Postoenko Yu, Talanov V (1999) Application of Complex Phase-Shift Keyed Signals in Seismic Sounding of Ground with a Hydroacoustic Source. Acoustical Physics 45(1): 1–12.
7. Lebedev A, Maryshev A (1998) Construction of Geological Cross-Sections Using Pseudo-Random Sequences [in Russian]. In: Ocean Acoustics. Proc. of the L.N. Brekhovskikh Workshop, GEOS, Moscow, pp 109–112.
8. Averbakh V, Artel’nyi V, Bogolyubov B, Bredikhin V, Lebedev A, Maryshev A, Talanov V (2008) In Situ Estimation of Crack Concentration in Hard Rock. Acoustical Physics 54(1): 84–96.
9. Bredikhin V, Lebedev A (2009) The Results of Measurements of the Acoustic Nonlinearity Parameter of Granite: Comparison of the Natural and Laboratory Experiment Data [in Russian]. In: Proc. of the 1st All-Russia Conf. “Problems in Mechanics and Acoustics of the Media with Micro- and Nano-Structure”, R.E. Alekseev Polytechnical University of Nizhny Novgorod, pp 31–38.
10. Averbakh V, Artel’nyi V, Bogolyubov B, Maryshev A, Postoenko Yu, Talanov V (2002) The Mobile Receiving and Transmitting Facility for Small-Depth Seismodiagnostics [in Russian]. In: Methods of Acoustic Diagnostics of Inhomogeneous Media, Institute of Applied Physics RAS, Nizhny Novgorod, pp 207–220.
11. Ghose R, Nijhof V, Brouwer J, Matsubaraz Y, Kaidaz Y, Takahashiz T (1998) Shallow to very shallow, high-resolution reflection seismic using a portable vibrator system. Geophysics 63(4), 1295–1309.
12. Averbakh V, Lebedev A, Maryshev A, Talanov V (2008) The diagnostics of
unconsolidated media acoustic properties in the field conditions. Acoustical Physics 54(4), 607–620.
13. Rudenko O, Vu C (1994) Nonlinear acoustic properties of a rough surface contact and acousto-diagnostics of a roughness height distribution. Acoustical Physics (40), 593–596.
14. Lebedev A, Beresnev I (2004) Nonlinear distortion of signals radiated by Vibroseis sources. Geophysics 69(4), 968–977.
15. Lebedev A, Beresnev I, Vermeer P (2006) Model parameters of the nonlinear stiffness of the vibrator-ground contact determined by inversion of vibrator accelerometer data. Geophysics 71(3), H25–H32.
16. Averbakh V, Artel’nyi V, Bogolyubov B, Virovlyansky A, Malekhanov A, Maryshev A, Talanov V (2005) A High-Power Intrawell Radiator of Shear Waves for Coherent Seismoacoustics. Acoustical Physics 51 (Appendix), 31–45.
17. Averbakh V, Lebedev A, Manakov S, Talanov V (2012) Phase method of cross-well profiling using coherent SH-waves. Acoustical Physics 58(5): 649–655.
18. Nikitin V (1981) Engineering seismic basics [in Russian]. Moscow State Univ., Moscow.
19. Konkov A, Lebedev A, Manakov S (2012) The reconstruction of the shear wave velocity profile and Poisson’s ratio based on the Rayleigh wave characteristics analysis. In: Proceedings of the XXV Session of the Russian Acoustical Society. Session of the Scientific Council of Russian Academy of Science on Acoustics. GEOS, Moscow, pp 233–237.





