Another most important type of waves primarily determining the nonlinear dynamics of the upper ocean is the internal waves (IW) that form in the region of the highest gradients of the vertically inhomogeneous density profile of the ocean water, i.e., in the pycnocline region. The basic role in the pycnocline formation is played by the stratification of the deep profile of temperature. This fact provided a basis for the creation of a large-scale laboratory model of the upper ocean, which was successfully implemented in the Large thermostratified tank of the IAP RAS under the supervision of V. I. Talanov.
Imaging of IW in the ocean, which exist due to its vertical density stratification, shows the presence of strongly nonlinear solitary pulses, the height of which can reach 50—100 m. They are described at the IAP RAS using various models: from weakly nonlinear ones based on the generalized Korteweg — de Vries and Gardner equations to strongly nonlinear ones (the Camasso — Choy and Ostrovsky — Grew models). These models are employed to study the conditions for existence of Riemann waves, solitons, and breathers of IW, their interaction with each other and with external fields. The soliton structure is determined by the signs of quadratic and cubic nonlinearity coefficients, while breathers are possible only for the positive coefficient of cubic nonlinearity. IW kinematic feature maps in the World Ocean are constructed. A model for the IW transformation in the shelf zone with allowance for the hydrology variability along the propagation path, for the Coriolis effects, and the dissipation was developed, which permitted one to numerically simulate the IW parameters in various shelves, including that of the Arctic basin, and to make a comparison with the imaging data. The physical mechanisms of the existence of anomalously large short-lived IW (counterparts of rogue waves) have been found out, namely, the modulation instability, the transformation on nonlinear "caustics", and the dispersion focusing; their possible appearance in the Baltic and South China Seas has been predicted
(E. N. Pelinovsky, T. G. Talipova, K. A. Gorshkov, and
I. A. Soustova).
|
|
Imaging of strongly nonlinear IW
in the eastern part of the Pacific Ocean
|
Atlas of IW propagation velocity (m/s)
in the World Ocean
|
Study of the interaction between waves of various spatial and temporal scales is prominent among the IAP RAS activities in the field of hydrophysics. The interaction of surface and internal waves is one of the most interesting examples of such an interaction under natural conditions. It is shown by the IAP RAS scientists that the physical mechanisms of the influence exerted by IW and IW-generated subsurface currents on wind waves are very different in various ranges of wind waves. In the meter and decimeter wavelength ranges, the determining role is played by the mechanism related to the direct effect of an IW-generated variable subsurface current on surface wave kinematics. An appropriate model for the variation of the wind wave field characteristics affected by IW was developed by the team headed by V. I. Talanov and called the kinematic model. This model has been confirmed by numerous laboratory and field experiments (V. V. Bakhanov) and is well known to specialists. In the high-frequency part of the wave spectrum (centimeter and millimeter ripples), of primary importance are other effects, in particular, the modulation of the damping coefficient of surface waves due to the redistribution of films of surface active substances under the action of IW (S. A. Ermakov). There is experimental evidence for an essential role of the cascade mechanisms of IW action on short (centimeter) wind waves: the current generated on the IW surface transforms meter and decimeter waves and they, in turn, affect centimeter ripples. Besides, the inhomogeneous current field generated by IW varies the wind velocity field over the water surface, which leads to the modulation of the small-scale wind-wave increment (Yu. I. Troitskaya).
|
|
IW soliton shapes
depending on the signs
of the nonlinearity coefficients
|
Comparison of data on imaging (red curve)
and simulating (black curve) an IW packet moved
to a distance of 14 km (the Portuguese shelf)
|
Study of the interaction between waves and inhomogeneous currents is also of great importance in hydrophysical research. Of special interest is the nonlinear interaction of IW with flows in the vicinity of the so-called critical layers, i.e., the resonance levels, in which the phase velocity of waves coincides with the flow velocity. This interaction can give rise to a significant restructuring of the current due to a return action of the wave on the current as a result of the resonance pulse exchange. In the quasi-linear model of a turbulent wake behind a body towed in a stratified liquid for large Reynolds and Froude numbers, developed by
Yu. I. Troitskaya, it is shown that the basic mechanism of the wake evolution is the development of a hydrodynamic instability of the jet flow excited by the body. Numerical and laboratory experiments confirmed the proposed model; the relevant results on the velocity field evolution in the wake (average parameters of the wake) are determined from the model with an accuracy of up to several percent.
Researchers have recently been interested in physical phenomena that occur when fresh wastewater discharges from the collector of an underwater relief system to the stratified ocean. The need to understand and predict these processes is due to urgent ecological problems and current development of aerospace remote-sensing monitoring of underwater systems of wastewater relief. Scale-model study in the LTST has shown that the buoyant jets formed in this process excite intense short-period IW in the interaction with the pycnocline. The wave generation mechanism related to the excitation of self-sustained oscillations of the globally unstable mode in the interaction of a buoyant jet with the pycnocline is proposed, which is based on analysis of the dependences of the generated wave amplitudes on the jet current characteristics and stratification (Yu. I. Troitskaya, E. V. Ezhova, V. I. Kazakov, and
D. A. Sergeev).
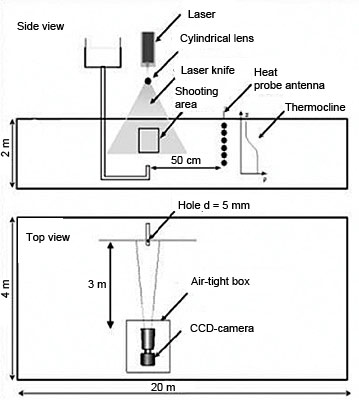 |
 |
Experimental design in the Large thermostratified tank
for studying the mechanism of IW generation by axially symmetric turbulent jets
|
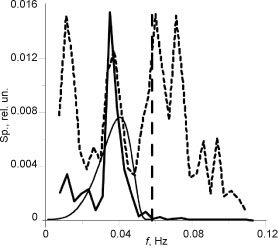
Spectra of jet oscillations (dashed line) and IW oscillations (solid line). The straight line shows the maximum buoyancy frequency, the curve corresponds to the frequency dependence of the excitation coefficient of the lower mode
|
To carry out a comprehensive study of the phenomena caused by submerged buoyant jets in a stratified fluid, a direct numerical simulation of the dynamics of the fountain formed by the penetration of a vertical jet through the pycnocline in a stratified fluid was made (O. A. Druzhinin). The calculations have shown that for the Froude numbers exceeding the critical value, self-sustained oscillations of the fountain occur, which are accompanied by IW generation in the pycnocline. The possible modes of fountain self-sustained oscillations and the corresponding structures of the generated IW are studied. It follows from the calculation data that the dependence of the oscillation amplitude of the fountain top on the Froude number well agrees with the predicted theoretical model of interacting mode competence in the soft excitation regime.
The fundamental results of theoretical and experimental investigations of the physical mechanisms
of the IW and inhomogeneous current effect on wind waves, obtained at the IAP RAS, were the basis for the development and practical use of radiophysical methods and facilities of remote diagnostics of the upper ocean.
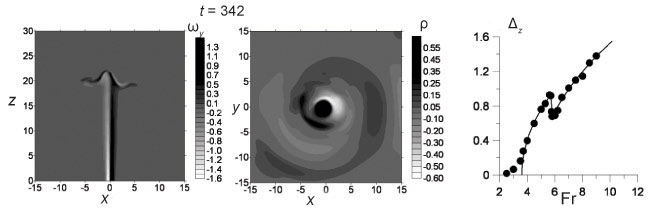 |
Vorticity fields (side view, in the axial plane of the fountain) and densities (top view, in the horizontal plane at the pycnocline level); the dependence of the fountain oscillation amplitude on the Froude number (right))
|





